Conway's "The Game of Life"

A fascinating, albeit old (late 60's/early 70's) idea in mathematics is the evolution of extraordinary complex systems from a few initial set rules and conditions.

One such fascinating example is Conway's "The Game of Life".

From the few initial rules below:   

   For a space that is 'populated':
        Each cell with one or no neighbors dies, as if by loneliness.
        Each cell with four or more neighbors dies, as if by overpopulation.
        Each cell with two or three neighbors survives.
    For a space that is 'empty' or 'unpopulated':
        Each cell with three neighbors becomes populated.

 follow strangely 'alive' patterns that resemble cells seen under a microscope.

Of course, there need to be the initial "seed cells", which determine which shapes will 'evolve' and which shapes will 'die off'.

If you've never tried or played with this, try it here or here . (*Note: both of these link to older webpages - circa early 2000 - and programmers aren't always artists or graphic designers. Don't be dissuaded, great ideas are great regardless of how ugly the webpage is. And also note there are hundreds, if not thousands, of similar applications on the net - a quick google search will turn them up for you.)

Having run the application you'll see a variety of shapes emerge from whatever initial "seed" you draw onto the page. 

Some of the more common ones:

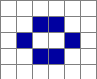
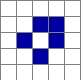
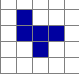
Above: The first 3 cells are static - having evolved they are no longer changing, unless they collide with  a larger and active body of cells. The 4th cell in is a 2 phase "Oscillator" - jumping between 2 states. Some groups of cells will find an equilibrium and oscillate between 2 or more shapes. The final group on the right represents f-pentomino - a simple starting position that gives rise to shapes and patterns that don't stabilize over 1000+ generations

Should you have difficulty getting started (ie: your first few attempts result in life "dying off" or stablizing too quickly to be of any interest), try the F-Pentomino shape, which evolves quickly and produces a wide variety of "lifeforms".

Now you should probably take a break from this post and play with the applications linked above before coming back and reading the rest of it - it'll make a lot more sense.

There are a variety of initial rules - elaborations upon Conway's basic rules, which give rise to even more interesting shapes and configurations - some resembling coral, others resemble arial views of cities and other geometric structures. And, depending on how fortunate you were in your initial "seeding" of the graph, you may have seen other such shapes as "gliders" and "spaceships" that wriggle across the screen like primitive forms of cellular life. But as intriguing as this is, note that the simulation you are running is 2 dimensional, presumes an initial cell shape that is square and a view of the universe that is essentially 2 dimensional (an X axis, a Y axis and the element of time). 

Now imagine this simulation run perhaps with different shapes - for example tiled triangles, hexagons, pentagons, whatever. 

And imagine that it's played in 3 dimensions - with an x, y and now z axis, over time. What patterns and shapes could you expect to see evolve then?

This game layed the foundation for Stephen Wolfram's theory that the universe itself is, in fact, a kind of "cellular automation".

Now, as thought provoking as this simulation is, it's only a simulation, really, a visual example of how extraordinarily complex patterns, shapes and "behaviours" can evolve from the simplest of rules and initial starting conditions. It has no practical purporse other than to illustrate this point. But it fascinates me nonetheless -  and here are a few of the reasons or possibilities I see in it:

1. Note there is no value within the game to survival - cells "live" and "die", but they on their own take no action - what if there were a rule in place, that when a group of cells reached a certain "size" (ie: 7-11-13 connected cells) they then began to take pains to ensure they did not die off or fall into a static state?
2. IN the simulation the only requirements for growth are space and an initial population of 3 cells. What if, for a cell to survive, it needed to consume another cell (and thereby grow into the bargain)? How could you programatically encode senses into the cells so that they could "read" the neighboring spaces and search for food?
   
3. What if the rules evolved along with the cells within the game - for example, at certain critical masses groups of cells would find themselves subject to different rules of growth and population - as in the real world? For example, cells in our bodies, microbes in the air, etc. are not subject in any great sense to the rule of gravity. But as they group together and form increasingly complex organisms the force of gravity becomes something to be reckoned with. In addition, how do cells on the interior of an organism arrange for delivery of food, and what is the simplest way programatically to allow for this eventuality? Or would it evolve?
   
4. And some of the above are covered in this, but what if, in every X generations of the simulation, or when cells reached again that critical mass or size, they were allowed to change the rules to favour their survival? To write their own rule(s) and append it to their own organization?
5. The simulation, as it is viewed in the links above, happens in 2 dimensions + time. We can visually imagine, and there are programs written, that replicate the simulation with various rules in 3 dimensions. But in the purest form the game does not require a graphical display, and computers can handle processing multi-dimensional arrays - as many as current technology will allow it to run. What if the the animation were run across 10, 100, 1000 dimensions, each "cell" possessed of n(^10Nth) "dimensions" - adding "dimensions" as it grew or ran out of "space" in the dimensions it occupied? What if the requirements were changed from "Space" on a graphical display to "space" on a hard-drive - or linked over the internet a variety of hard drives - with both survival and the acquisition of knowledge/information it's initial conditions? What if it were given the ability to write and rewrite (making it more compact, freeing space and allowing for it's growth) it's own source code? Could it be expected we would at any time see anything approaching intelligence or evolution?

Those are just a few of the possibilities inherit in the simulation. Note that on a computer it would quickly fill the hard-drive, the challenge would then be to somehow limit the "evolution" to those groups of cells or ideas you thought had the most potential.

Trivia: When Conway first devised the game he ran the simulations over a "Go" gameboard, and by drawing the cells on a blackboard and erasing them. There weren't computers (not household, anyways) back then.