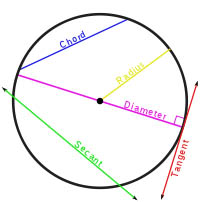
 Consider the circle. In it are embodied a multiplicity of ideas and questions - emblematic of perfection, (think of the Halo), of completeness, the perfect 2 dimensional shape (and in 3 dimensions the Sphere, but arguable the Sphere stems from the circle and so we'll limit ourselves here). There is no way to accurately - precisely - calculate it's area - PI being only an approximation, an irrational number, yet it's appearance belies it's complexity.
Consider the circle. In it are embodied a multiplicity of ideas and questions - emblematic of perfection, (think of the Halo), of completeness, the perfect 2 dimensional shape (and in 3 dimensions the Sphere, but arguable the Sphere stems from the circle and so we'll limit ourselves here). There is no way to accurately - precisely - calculate it's area - PI being only an approximation, an irrational number, yet it's appearance belies it's complexity.
Think of a circle in motion, rotating around a central axis. An infinitely large circle - at it's center - absolute center, there is a point of absolute rest - no motion whatsoever. And then it's diameter, drawn far enough out, vastly exceeding the speed of light and as a consequence going back through time.
Or if this is too much consider that there's no simple way - in fraction or decimal - to express PI. There therefore can be no circle whose area is a whole number - by definition it will always involve some uncertainty or remainder.
Or consider some of the open questions about PI, reprinted here from Pi History:
- Does each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 each occur infinitely often in π?
- Brouwer's question: In the decimal expansion of π, is there a place where a thousand consecutive digits are all zero?
- Is π simply normal to base 10? That is does every digit appear equally often in its decimal expansion in an asymptotic sense?
- Is π normal to base 10? That is does every block of digits of a given length appear equally often in its decimal expansion in an asymptotic sense?
Links: Wiki on the Circle & Squaring the circle